- Основные принципы
- Построение системы контуров
- Использование планарных графов
- Метод выделения максимального дерева
- Построение системы уравнений
- Оптимизированная процедура составления системы
- Формальный подход
- Пример системы уравнений
- Ветвь электросхемы
- Узел цепи
- Что такое контур
- Определение
- Формула первого правила Кирхгофа
- Для трёхфазной сети
- Расчеты электрической цепи с помощью первого закона Кирхгофа
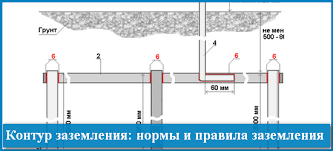
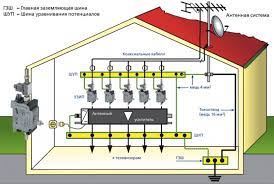
- Расчёт электропроводки
- Расчёт блока питания
Основные принципы
Любая электрическая цепь состоит из участков (ветвей), образующих узлы и цепи. Для определения значений тока через какой-либо элемент используются два закона Кирхгофа. Прямая формулировка уравнений дает систему с максимальным их числом, равным числу ветвей.
В результате, если множество узлов цепи равно Y, а количество ветвей равно P, уравнения распределяются следующим образом:
- Для узлов У-1 по закону Кирхгофа для токов;
- Для ветвей R-U+1 по закону Кирхгофа для напряжений.
Это число является избыточным и приводит к формированию громоздкой системы уравнений большой размерности.
Для упрощения расчетов разработаны методы, позволяющие сократить количество уравнений до допустимых значений без снижения точности результатов. Самым простым методом является метод контурного тока.
Построение системы контуров
Самая большая сложность заключается в правильном выборе контуров. Количество контурных токов будет равно количеству выбранных контуров.
Важно! Каждый элемент схемы должен быть частью хотя бы одной цепи.
Существует два распространенных метода выделения контуров.
Использование планарных графов
Метод планарного графика используется для ручных расчетов, так как он самый простой и интуитивно понятный. Для построения планарного графа диаграмму рисуют таким образом, чтобы не было взаимного пересечения ветвей. Получается, что схему можно разделить на несколько ограниченных участков, образующих контуры.
Рассматриваемый метод неприменим без дальнейших преобразований, если форму невозможно выразить в виде планарного графа.
Метод выделения максимального дерева
Метод выбора максимального дерева является более абстрактным и используется для автоматизированных расчетов и наличия специализированных программ. Суть метода заключается в исключении некоторых ветвей из цепочки в соответствии со строгими правилами, которые заключаются в следующем:
- На каждом шаге исключается только одна ветвь;
- Устранение ветки не должно приводить к разбиению графа на несколько частей или к «висячим узлам»;
- Количество внешних звеньев равно количеству независимых каналов;
- подключение к внешней ветке образует соответствующий цикл.
Построение системы уравнений
От чего зависит сопротивление проводника
Построение системы уравнений по рассматриваемому методу осуществляется по следующим правилам:
- Для каждого выбранного контура задается направление орбиты;
- В левой части уравнений записывается сумма всех произведений искомых токов в ветвях на сопротивления ветвей. Сумма источников напряжения, присутствующих в цепи, записана справа;
- Если направление искомого значения или источника напряжения совпадает с заданным направлением обхода, члены записываются со знаком плюс, в противном случае имеют отрицательное значение;
- Величина токов в ветвях заменяется их выражением в виде петлевых токов.
После выполнения арифметических операций (раскрытие скобок, сокращение однородных членов) получается система уравнений, в которой неизвестными величинами являются виртуальные петлевые токи.
Путем решения системы уравнений получаются значения контура, а затем искомые значения.
Оптимизированная процедура составления системы
Упрощенный метод заключается в следующем:
- В уравнениях в левой части записано произведение суммы всех сопротивлений, входящих в цепь, на ток цепи;
- Из полученного выражения вычесть токи соседних шлейфов, умноженные на сумму сопротивлений общей ветви;
- Справа записана сумма источников ЭДС цепи.
Формальный подход
Формальный подход предполагает матричную форму системы уравнений. Для расчетов первые данные записываются в матричном виде. Используются следующие матрицы:
- C — где имеется i строк, соответствующих количеству контуров, и j столбцов, соответствующих количеству ответвлений;
- Z — диагональная матрица сопротивлений, где количество строк и столбцов соответствует количеству ветвей;
- Ct — транспонированная матрица C;
- I — матрица контурных значений;
- J – матрица источников тока;
- E – матрица ЭДС.
При составлении массива C каждый элемент Cij будет:
- 0, если ветвь j не входит в контур;
- -1, если ответвление входит в цепь, направление тока противоположно цепи;
- 1 — то же, но направление тока совпадает с контуром.
В матрице Z диагональные элементы равны сопротивлениям секций, остальные равны нулю.
Окончательная формула для расчетов:
C∙Z∙Ct∙I=C(Z∙J+E).
Эта форма записи решения в матричной форме показывает, как выполняются операции над скомпилированными матрицами.
Пример системы уравнений
Ниже приведен пример расчета конкретной схемы без учета номиналов элементов.
Пример решения
В данной цепи выделены три цепи. Как выразить токи в ветвях через контур:
- i1=I1;
- i2=I2;
- i3=I3;
- i4=I2+I3;
- i5=I1+I2;
- i6=I1-I3.
Как написать систему уравнений:
- i1R1+i5R5+i6R6=E1;
- i2R2+i4R4+i5R5=E2;
- i3R3+i4R4-i6R6=0
Чтобы заменить значения контура:
- I1R1+(I1+I2)R5+(I1-I3)R6=E1;
- I2R2+(I2+I3)R4+(I1+I2)R5=Е2;
- I3R3+(I2+I3)R4-(I1-I3)R6=0
После преобразования получается искомая система уравнений:
- (R1+R5+R6)I1+R5I2+R6I3=E1;
- R5I1+(R2+R4+R5)I2+R4I3=Е2;
- -R6I1+R4I2+(R3+R4+R6)I3=0.
Система трех уравнений легко решается после подстановки известных параметров. Из полученных значений токов контура можно затем найти нужные значения.
Данный пример решения задач методом контурных токов показывает, что любую достаточно сложную схему можно значительно упростить для решения, руководствуясь инструкцией.
Важно! Метод неприменим, если невозможно преобразовать цепь без взаимной обрезки ветвей.
В некоторых случаях схему можно упростить, преобразовав ветви, соединенные по схеме «звезда», в треугольник.
Точно такие же результаты дает метод узловых потенциалов. Расчеты основаны на поиске потенциала каждого узла (так называемого узлового потенциала). Существуют программы, позволяющие рассчитать параметры онлайн по рассмотренным методикам.
Читайте также: Торцовочная пила Metabo: ТОП-10 моделей и как выбрать комбинированный инструмент, характеристики устройств и отзывы покупателей
Ветвь электросхемы
Это основной элемент цепи, по которому протекает тот самый ток. В простейшем случае это отрезок провода, отводом также является включенный в розетку электроприбор и кабель, который к этой розетке подходит.
Каждая из ветвей, в свою очередь, может быть разделена на несколько новых ветвей в узлах. Ветви могут быть соединены параллельно, в узлах и последовательно. В последнем случае они образуют новую более крупную ветвь.
Узел цепи
Место соединения ветвей электрической цепи называется узлом. Закон Кирхгофа для электрической цепи описывает распределение тока в разных ветвях, соединенных с одним и тем же узлом.
что такое узел электрической цепи что такое узел электрической цепи первый закон кирхгофа — узел электрической цепи первый закон кирхгофа — узел электрической цепи
В терминах электропроводки узел — это соединение нескольких проводов с автоматом или с клеммой, а также розетка или двойная розетка.
Что такое контур
Все электрические сети включают в себя источник питания. В электрическом фонарике это аккумулятор, и всю цепь можно проследить визуально, а в системе электроснабжения жилого дома – это подстанция, которая может находиться за несколько километров.
В таких сетях мощность источника тока во много раз превышает мощность квартирной проводки, поэтому при проектировании электропроводки параметры трансформатора не учитывают, а расчет производят только для цепи, включающей несколько узлов.
Определение
Первый закон Кирхгофа для электрической цепи основан на законе сохранения заряда или законе сохранения энергии. Согласно этим законам, количество «электричества», входящего в узел, должно равняться количеству выходящего из него.
Таким образом, это правило имеет две формулировки:
- Нет. 1. Алгебраическая сумма токов в узле равна нулю. Это алгебраическая сумма, где положительное значение «+» имеет ток, направленный в узел, а отрицательное значение «-» — ток, вытекающий из узла. Эта формула используется при расчетах сложных схем.
- Нет. 2. Сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Это арифметическая сумма без учета знака значения
Важно! В сетях переменного тока, особенно высокочастотных, есть потери, связанные с емкостью линии. Величина этих потерь не может быть измерена прямыми методами, что приводит к явному нарушению первого закона Кирхгофа.
Формула первого правила Кирхгофа
Как и любой другой закон электротехники, 1 закон Кирхгофа выражается формулой, имеющей два варианта написания. Например, можно взять узел с двумя входящими проводами и токами в них I1 и I2 и тремя исходящими проводами I3, I4 и I5:
- Алгебраическая сумма. Получается преобразованием предыдущей формулы Σk-Σm=0 или I1+I2-I3-I4-I5=0. Это выражение используется при сложных расчетах электронных схем.
- Арифметическая сумма. Σk=Σm или I1+I2=I3+I4+I5. Здесь k входящие линии и m исходящие. Эта формула используется при определении сечения токопроводящих проводов для однофазной проводки или однолинейной схемы систем электроснабжения, а также необходимой мощности источников питания.
Такие уравнения составляются для каждого узла в сети, причем нижестоящий узел является ответвлением вышестоящего узла. Это можно увидеть, когда вы рисуете однолинейный график.
Информация! Ток в приходящих проводах считается положительным, а в отходящих — отрицательным.
Для трёхфазной сети
Чаще всего трехфазные сети переменного тока выполняются по схеме с рабочей нейтралью. В этом случае пересечение фазных проводов с нулем является узлом и подчиняется первому правилу Кирхгофа, но эта формула имеет более сложный вид.
Дело в том, что в сетях переменного тока помимо активных протекают реактивные, индуктивные или емкостные токи. В результате ток в проводах по разным фазам смещается не на 120°, а на разную величину.
Для расчетов в таких сетях рисуется векторная диаграмма и при расчете значения тока в нейтрали добавляется не значение тока, а соответствующий вектор ↑In=↑Ia+↑Ib+↑Ic.
Ввиду сложности такого расчета, как правило, его не проводят, а вместо этого нагрузку распределяют по фазам как можно более равномерно, а сечение нулевого проводника выбирают не , а предлагаемое производителей кабельно-проводниковой продукции.
Расчеты электрической цепи с помощью первого закона Кирхгофа
Первый закон Кирхгофа используется для расчета силы тока и сечения электрических проводов и мощности источников питания.
Расчёт электропроводки
Кабельные линии и линии электроснабжения имеют форму дерева — кабель большего сечения и силы тока делится в узле на несколько ветвей меньшего сечения и силы тока. В этом случае Iвх = ΣIвых.
Например, при подключении к линии электроприборов с номинальным током 5 А, 4 А и 2 А ток в подходящем кабеле будет Iвх = 5 + 4 + 2 = 11А.
Расчёт блока питания
Большинство электроприборов подключаются напрямую к сети переменного тока 220 В, но есть устройства, требующие пониженного напряжения. Такие устройства подключаются к источникам питания.
Например, есть два источника постоянного напряжения 12 В с током 1,5 А и 2,5 А. Нужно выяснить, какую светодиодную ленту можно подключить к этим устройствам, если они соединены параллельно.
Этот расчет производится по формуле Iвых=ΣIвх=1,5А+2,5А=4А. Поэтому ток потребления этого диапазона не может быть больше 4 А или 48 Вт.